B 树的结构和算法

前面我们只是简单的介绍了一下 B 树，现在就开始展开聊一聊这个经典的数据结构。B 树可能会由很多个节点组成，每一个节点可能会保存着 N 个 key 和 N + 1 个指针指向子节点，他们大致可以分为三个大类：

• 根节点，也就是最顶点的节点，它没有父节点；
• 叶子节点，也就是最底部的节点，它没有子节点；
• 内部节点，也就是中间部分的节点，他们连接起了根节点和叶子节点，一般来说内部节点可能会有好几层。

B 树的每一个节点，是既需要存储 key 也需要存储 value 的，其中这些 key，就是我们搜索时用来比较的键，也就是这些键，将树分为了多颗子树，这些 key，也必须要是有序的，这样我们才能使用二分搜索进行查找。

我们管每个节点最多能放下多少的 key 这个容量，叫做 degree, 当然前面我们也说过这个也可以叫这颗树的 fanout，每个节点最多允许要多少个子节点，叫做 order。而每个节点，或者说每个页，他们的大小和实际上放着多少的 key 的这个比值关系，叫做 occupancy。

一颗 order 为 m 的 B 树必须要满足下面的几个条件：

• 每一个节点最多可以有 m 个子节点；
• 根节点最少要有 2 个子节点，除非它也是叶子节点；
• 内部节点最少要有 m/2 个子节点；
• 所有的叶子节点要在同一层，即高度要一致；
• 非叶子节点有 k 个子节点的话那需要有 k-1 个 key。

如果是一颗 order 为 7 的 B 树，那么内部节点可以拥有 7/2 到 7 个子节点，因此可以有 3，4，5 或者 6 个 key。而根节点，可以有 1-6 个 key。

我们再看仔细看看之前贴的一张来自维基百科的图：

出于简化，这里只展示了 key 值，不过没关系，意思是差不多的。

• 根节点的第一个 key 是 7，而第一个指针则指向了包含所有小于 7 的 key 的子树；
• 第二个指针指向了所有 7 和 16 之间的子树；
• 第三个指针则指向了所有大于 16 子树;
• 子节点的数量（即指针的数量）总是比 key 的数量多一；
• 所有的叶子节点都在第二层同一高度。

一个节点里存放的数据里，指向子节点的指针和 key 交替出现，并且他们满足一个有序的关系。

了解完 B 树大概是个什么结构以后，就可以看看 B 树中是针对查找、插入和删除的算法都是如何工作的。这里强烈建议可以先在这里通过一个可视化的方式查看 B 树和 B+ 树都是如何工作的。

B 树的查找算法还是非常简单的，其实就是从根节点开始，通过比较 key 的值进行二分搜索，找到对应的子树，然后不断重复这个过程。难点主要在于如何插入和删除的过程。

当要插入一个值到 B 树中时，需要先通过查找过程首先定位到要插入的正确位置，如果插入后这个节点已经超过了我们规定的大小，需要进行一个分裂操作，或者更准确来说，碰到下面的情况时需要进行分裂：

• 对于叶子节点，假设节点可以放下 N 个键值对，再插入的话已经超过了这个 N；
• 对于内部节点，除了键值对我们还要考虑其中存储的指针数量，假设节点可以放下 N + 1 个指针，超过 N + 1 的话也要进行分裂。

分裂的操作具体是这个样子的：

• 先将超过规定容量的节点分为左右两个节点；
• 将中间的数据提升到父节点；
• 如果父节点也超过了规定的容量，需要将父亲节点也进行分裂；
• 沿着树向上一直进行这个操作，直到都满足要求为止。

以下面的图为例子，其中 11 是新插入的数据，13 是被提升到父节点的数据，对于叶子节点：

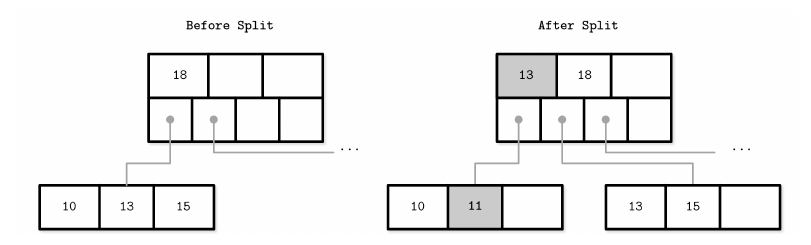
对于内部节点：

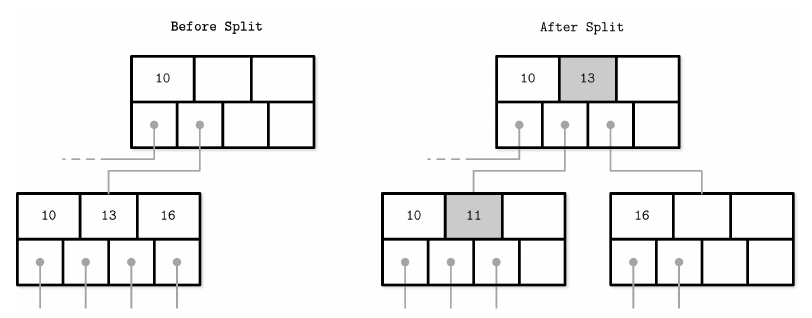
和插入操作类似，删除操作也可能需要进行重新平衡的操作，不过我们这里先不管，因为对于数据存储来说，为了减少一点代码的复杂度，删除的数据我们完全可以直接将其标记为已删除的状态，留下一个 “墓碑” 放在原来的位置，读取的时候跳过，而需要写入的话直接覆盖上去新数据就可以了。

当然，光了解 B 树的结构和算法是不够的，因为我们要实现一个基于磁盘的结构，而磁盘的读取和内存内直接读取数据是完全不一样的，必须要像前面那样依赖 fs.readSync 这样的接口通过指定文件的偏移量来读取指定大小的数据块，因此我们还需要设计一个简单好用的存储格式，接下来我们就来详细讲一讲存储的格式。