B 树和数据页

前面利用一个简单的哈希索引实现了一个简单的数据库，虽然针对单个键的查询效率非常高，但还存在很多的问题。比如键特别多，范围查询效率差，没有持久化索引等等。要解决这些问题，就必须要引入新的数据结构。

我们经常接触的更多的是在内存中的数据结构，内存相比硬盘离 CPU 更近，访问速度要快的多，但对于数据存储这个场景来说，很多时候数据量大到无法放进机器的内存中，因此必须要有一个基于磁盘的数据结构，我们一次只加载一小点进来用于缓存或者比较，而绝大部分的数据都继续放在磁盘上。

需要设计一个基于磁盘的数据结构，势必要求对硬件有一定的了解的，事实上硬件也确实会很大程度上影响到软件的设计，绝大多数老牌数据库的设计都受到当时主流的机械硬盘设计的影响。而像闪存等新的存储硬件的出现也极大地影响着新出现的数据库的设计。

机械硬盘有点类似唱片机一样的有着圆形盘片和读写头，在读写数据时需要让读写头先找到特定的位置，这个叫寻道，然后才能开始读写数据，也就是说随机访问会存在一定的成本，但接下来的顺序读写会相对很快。机械硬盘最小的读写单位是一个 Sector，一般大概是在 512 bytes 到 4kb 之间。

而固态硬盘（SSD）就没有这样的物理结构，它使用闪存芯片来作为存储单元，而闪存会分为固定的区块为单位进行管理：

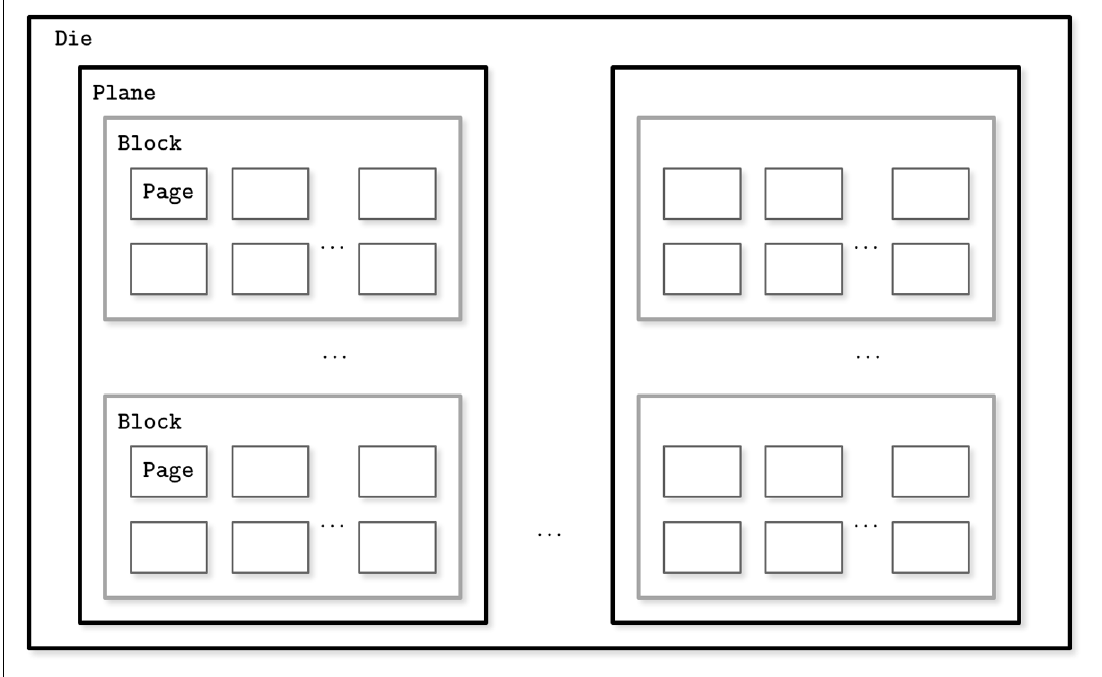
其中最小可写入的区块是一个 Page，一般在 2- 16 kb 之间，而最小可以擦除的区块，是一个 Block，一个 Block 可能会包含 64 到 512 个 Page。

对于这二者来说，有一个共同点就是我们的读写操作每次都是需要基于一小块内容的，而不是单独的一个个字节。 因此设计针对磁盘的数据结构时，我们最好利用这个特点，也像磁盘的设计一样，去读写固定一小块完整的内容，而不是任意字节大小的内容，这一块内容里可以包含一个指针，告诉我们下一次需要读取的内容在哪个位置，然后再到那个位置再把一整块内容读取进来。

接下来仔细考虑数据结构的设计，除了像哈希索引这样常数级别的的查询效率，还有一类数据结构虽然差一点点，但也有很高的效率，那就是树形结构。例如最普通的二叉搜索树，理想情况下拥有对数级别的效率，但二叉搜索树在这个场景下也有点问题，单纯的二叉搜索树可能是不平衡的，这个平衡的意思就是说，他的每个子节点的大小是差不多的或者说左右子树的高度是差不多的，不要一边很大一边很小。在最极端的情况下，二叉搜索树甚至会形成一个链表的样子，导致查询变成了线性的效率。

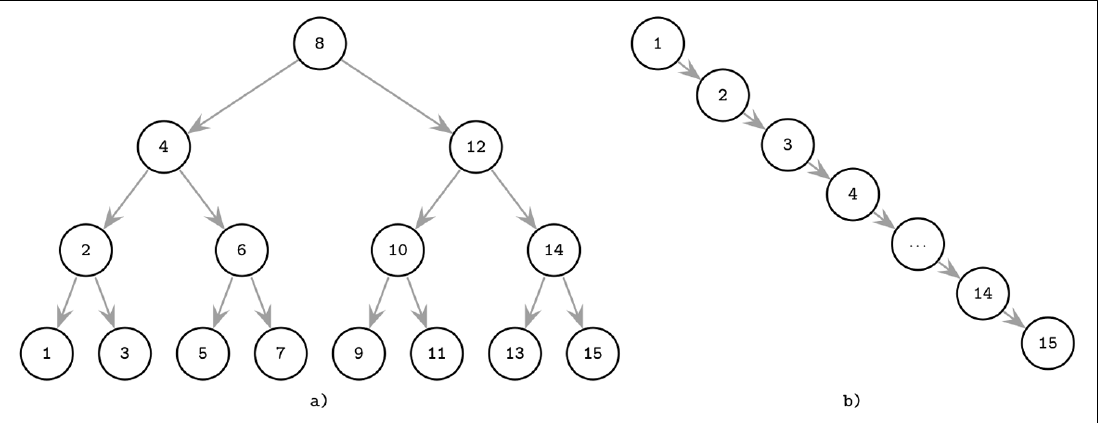
因此我们需要它是尽可能保持平衡的，但只是对平衡有要求的话，我们有 AVL 树和红黑树呀，他们是否满足要求呢，深入想一想还是会有问题，他们都是二叉树的一种，每一个节点只能存一个值，如果数据量大了，这棵树可能会特别高，在内存中还好，但在硬盘上的话访问一次节点就要需要一次磁盘 I/O，这就有点浪费了，而且因为数据插入的时候是一个随机的顺序，因此对于二叉搜索树来说新加的节点在磁盘上并不一定会挨着它的父节点，也就是说父节点包含的两个子节点他们在磁盘上可能隔着十万八千里，而前面我们知道对磁盘来说这种频繁的随机位置访问性能是比顺序访问要更差的。

因此我们希望它的节点可以再“胖”一点，里面多放一点东西。这个胖瘦的程度呢，也有个专门的名字，叫做 fanout (扇出)，就是一个节点最多允许有几个子节点。 fanout 越大的话，这样树的高度就没那么高了，会变得更“扁”。对存储在磁盘上的结构来说：

• 越高的 fanout 意味着相邻的键可能会尽量都挨着一起
• 越低的树的高度越能减少查询的时候访问磁盘的次数

这就引出了我们要讲的 B 树，你可能会听说过 B+ 树，它基于 B 树做了一些改进，这里先不管，在这么多年的使用过程中为了优化它其实诞生了很多的变种，我们这里先用 B 树这个词指代整个这一类的一大家子的树形结构，它的最主要特点就是高扇出的多路树（High fanout multiway trees）。

B 树

有点让人意外的是其实 B 树这样的结构我们在日常生活中经常会接触，最典型的就是目录这个东西，比如说一本英文词典，它收录了成千上万个单词，将他们按字母顺序排列起来。我们可以想象把所有的单词让他们像人一样站成一排，然后我们让其中每个字母开头的第一个单词向前进一步，这就形成了两排的结构，如果要查找某一个单词，只要知道它的首字母那我就知道它一定位于第一排的两个单词之间了。为了更进一步提高效率我们还可以构造一个多级目录，一层一层下去很快就能找到目标了。

一个典型的 B 树是下面这样子的，注意它一定是有序的，这样才能方便我们进行查找：

因为我们会把 B 树存储在磁盘上，一般来说其中的一个节点，会当成一个页来存储在磁盘上，所以有时候节点（Node）和页（Page）这两个词它可能是一个意思。

B 树的节点可以分为内部节点和叶子节点，其中叶子节点就是最末端的节点，它只存储了数据，没有存指针，也就是说没有子节点了。有的变种会让内部节点只存一个比较的 key，而数据全部放在叶子节点里，然后叶子节点之间用指针连接起来形成一个单向或者双向链表，这样范围查询的时候就非常方便，不需要再先回到父节点。

B 树最有意思的是，它的构造是自底向上的，像二叉搜索树这样的往往是自顶向下的，B 树在插入一个值时会先到最底部的叶子节点，当这个叶子节点超过了我们规定的大小，也就是说太胖了，才会进行分裂，然后开始向上冒泡，从而改变内部节点和树的高度。 你可以点击这里查看一个非常方便的针对 B 树的各种操作的可视化实现。

接下来我们就来一步步实现一个 B 树。